DEVELOPMENTS AND INTERSECTIONS
Sheet metal drawings are also known as sheet metal developments and pattern drawings, and we may use all three terms in this chapter. These terms are used because the layout, when made on heavy cardboard, thin metal, or wood, is often used as a pattern to trace the developed shape on flat material. These drawings are used to construct various sheet metal items, such as ducts for heating, ventilation, and air-conditioning systems; flashing, valleys, and downspouts in buildings; and parts on boats, ships, and aircraft.
A sheet metal development serves to open up an object that has been rolled, folded, or a combination of both, and makes that object appear to be spread out on a plane or flat surface. Sheet metal layout drawings are based on three types of development: parallel, radial, and triangulation.
The most common method to create simple sheet metal development drawings is by manual drafting and sketching methods. Sheet metal drafting/sketching templates are designed to facilitate layouts of sheet metal air conditioning and heating conduits and are available from manufacturers like Rapidesign®, Pickett®, Staedtler-Mars®, and Timely®. Computer-aided drafting (CAD) accelerates the sheet metal development design and template drawing process. CAD enables designer the flexibility to work with any CAD data to create, edit, and prepare models for high precision sheet metal fabrication. Sheet metal development CAD programs may be standalone software packages or add-on packages to powerful CAD applications such as AutoCAD®.
LEARNING OBJECTIVES
When you have completed this chapter, you will be able to do the following:
1.Recognize sheet metal developments.
2.Recognize the differences among parallel developments.
3.Recognize the differences among radial developments.
4.Recognize the differences among triangular developments.
SEAMS, JOINTS, AND EDGES
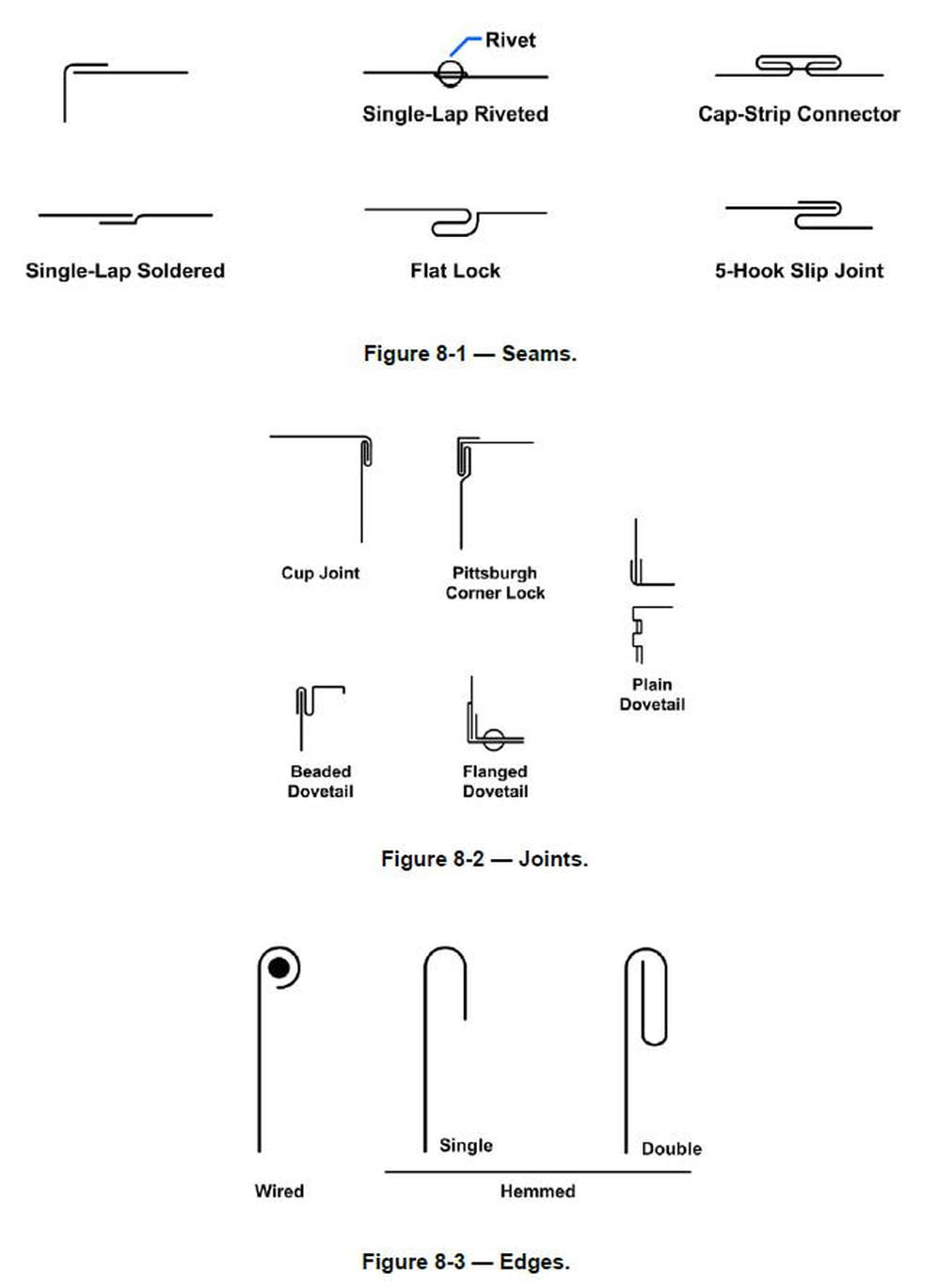
A development of an object that will be made of thin metal, such as a duct or part of an aircraft skin, must include consideration of the developed surfaces, the joining of the edges of these surfaces, and the exposed edges. The drawing must allow for the additional material needed for those seams, joints, and edges.
A variety of ways to illustrate seams, joints, and edges are shown in Figures 8-1 through 8-3. Seams are used to join edges. The seams may be fastened together by seams, solder, rivets, adhesive, or welds. Exposed edges are folded or wired to give the edges added strength and to eliminate sharp edges.
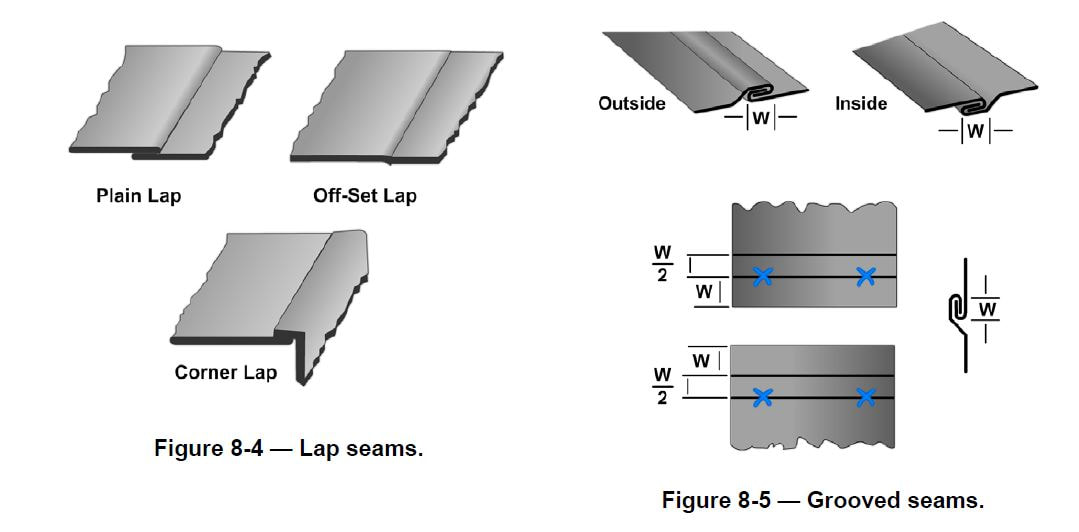
There are three types of lap seams: the plain lap seam, the offset lap seam, and the corner lap seam (Figure 8-4). Lap seams can be joined by drilling and riveting, by soldering, or by both riveting and soldering. To figure the allowance for a lap seam, you must first know the diameter of the rivet that you plan to use. The center of the rivet must be set in from the edge a distance of 2 1/2 times its diameter; therefore, the allowance must be 5 times the diameter of the rivet that you are using.
Grooved seams are useful in the fabrication of cylindrical shapes. There are two types of grooved seams: the outside grooved seam and the inside grooved seam (Figure 8-5). The allowance for a grooved seam is three times the width (W) of the lock. One-half of the total allowance width is added to each edge. For example, if you are to have a 1/4 inch grooved seam, 3 x 1/4 = 3/4 inch, or the total allowance; 1/2 of 3/4 inch = 3/8 inch, or the allowance that you are to add to each edge.
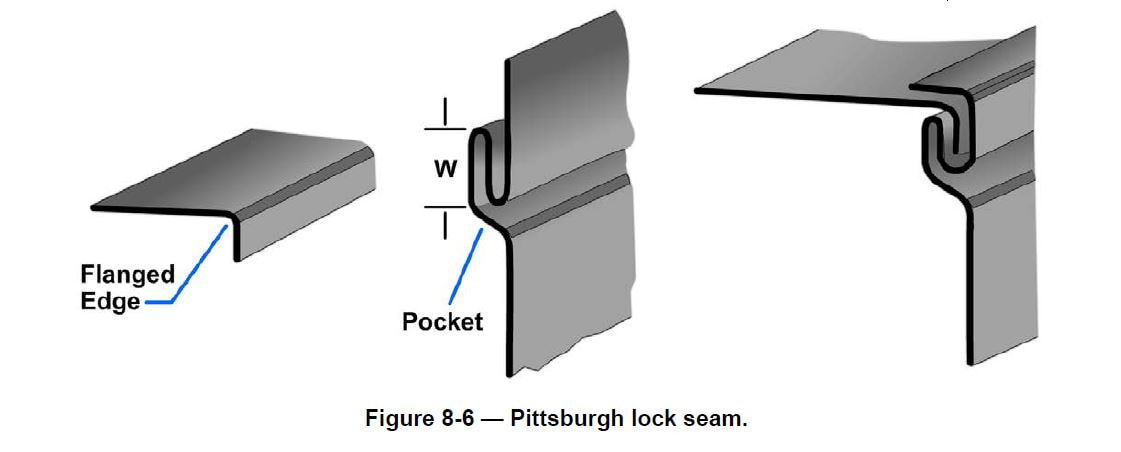
The Pittsburgh lock seam (Figure 8-6) is a corner lock seam. This seam is used as a lengthwise seam at corners of square and rectangular pipes and elbows as well as fittings and ducts.
The Pittsburgh lock seam (Figure 8-6) is a corner lock seam. This seam is used as a lengthwise seam at corners of square and rectangular pipes and elbows as well as fittings and ducts.
The Pittsburgh lock seam can be made in a brake but it has proved to be so universal in use that special forming machines have been designed and are available. The lock seam appears to be quite complicated, but like lap and grooved seams, it consists of only two pieces. The two parts are the flanged, or single, edge and the pocket that forms the lock. The pocket is formed when the flanged edge is inserted into the pocket, and the extended edge is turned over the inserted edge to complete the lock.
Note that most of the sheet metal developments illustrated in this chapter do not make any allowances for edges, joints, or seams. However, the designer who lays out a development must add extra metal where needed.
BENDS
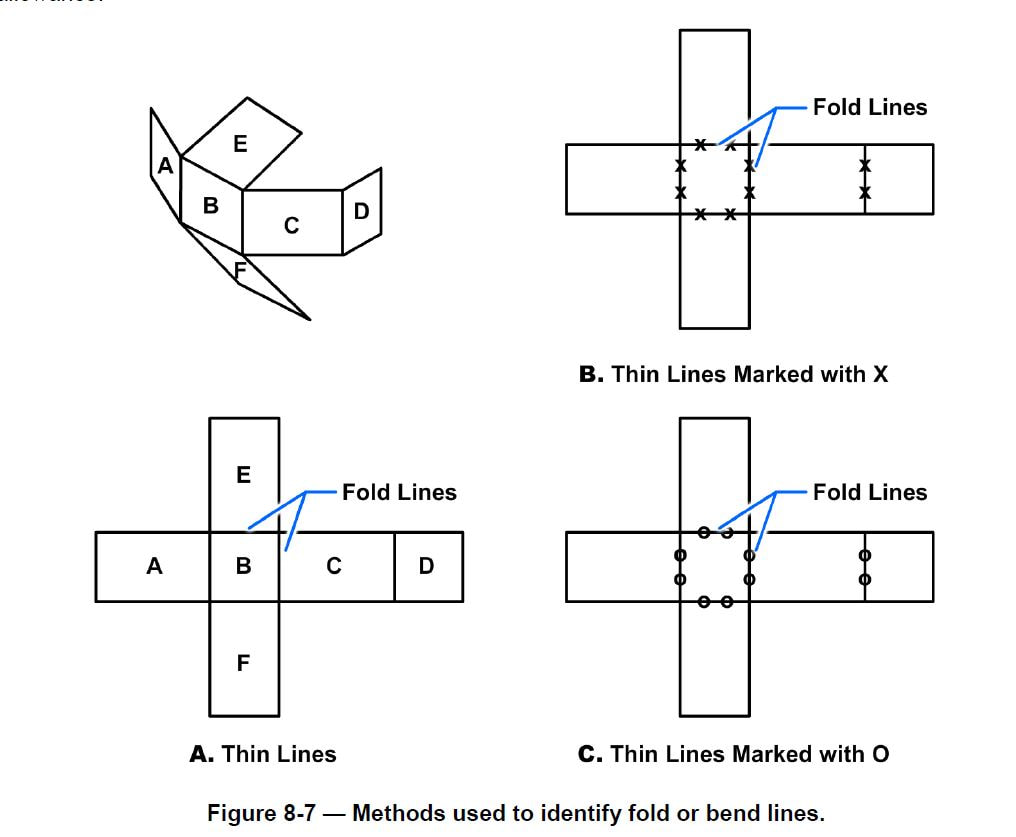
The designer must also show where the material will be bent, and Figure 8-7 shows several methods used to mark bend lines. If the finished part is not shown with the development, then drawing instructions, such as “bend up 90 degrees,” “bend down 180 degrees,” or “bend up 45 degrees,” should be shown beside each bend line.
When bending metal to exact dimensions, the amount of material needed to form the bend must be known. The term for the amount of material that is actually used in making the bend is known as bend allowance.
Note that most of the sheet metal developments illustrated in this chapter do not make any allowances for edges, joints, or seams. However, the designer who lays out a development must add extra metal where needed.
BENDS
The designer must also show where the material will be bent, and Figure 8-7 shows several methods used to mark bend lines. If the finished part is not shown with the development, then drawing instructions, such as “bend up 90 degrees,” “bend down 180 degrees,” or “bend up 45 degrees,” should be shown beside each bend line.
When bending metal to exact dimensions, the amount of material needed to form the bend must be known. The term for the amount of material that is actually used in making the bend is known as bend allowance.
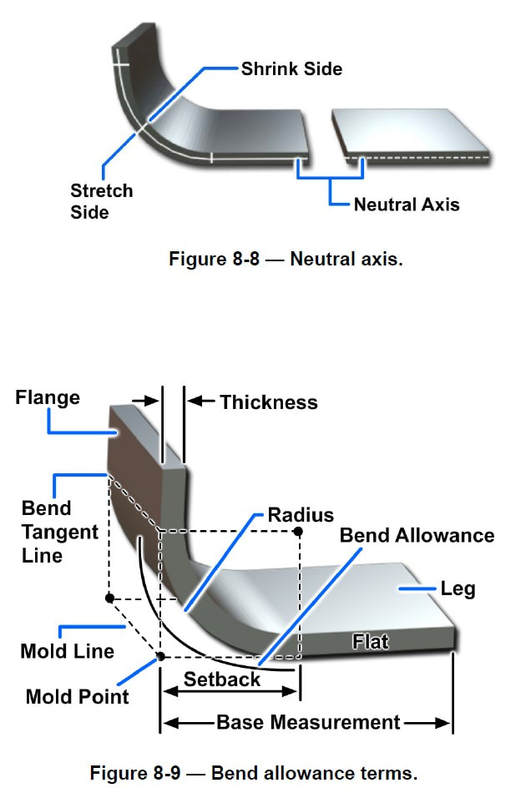
Bending compresses the metal on the inside of the bend and stretches the metal on the outside of the bend. Approximately halfway between these two extremes lays a space that neither shrinks nor stretches. This space is known as the neutral line or neutral axis (Figure 8-8). It is along the neutral axis that bend allowance is computed.
Bend Allowance Terms
It is important to be familiar with the following terms related to a bending job. The bend allowance terminology location is illustrated in Figure 8-9.
• Bend allowance—is the amount of material consumed in making a bend.
• Leg—is the longer part of a formed angle.
• Flange—is the shorter part of a formed angle, the opposite of leg. If each side of the angle is the same length, then each is known as a leg.
• Flat—is that flat portion not included in the bend. It is equal to the base measurement minus the setback.
• Base measurement—is the outside dimension of a formed part. Base measurement will be given on the drawing or blueprint, or it may be obtained from the
original part.
• Setback (SB)—is the distance from the bend tangent line to the mold point. In a 90-degree bend, SB = R + T (radius of the bend plus thickness of the metal). The setback dimension must be determined prior to making the bend because setback is used to determine the location of the beginning bend tangent line.
• Radius (R)—of the bend is always to the inside of the metal being formed unless otherwise stated. The minimum allowable radius for bending a given type and thickness of material should always be determined before proceeding with any bend allowance calculations.
• Mold line—is the line formed by extending the outside surfaces of the leg and the flange. (An imaginary point from which real base measurements are provided on drawings.)
• Bend tangent line—is the line at which the metal starts to bend and the line at which the metal stops curving. All the space between the bend tangent lines is the bend allowance.
Bend Allowance Terms
It is important to be familiar with the following terms related to a bending job. The bend allowance terminology location is illustrated in Figure 8-9.
• Bend allowance—is the amount of material consumed in making a bend.
• Leg—is the longer part of a formed angle.
• Flange—is the shorter part of a formed angle, the opposite of leg. If each side of the angle is the same length, then each is known as a leg.
• Flat—is that flat portion not included in the bend. It is equal to the base measurement minus the setback.
• Base measurement—is the outside dimension of a formed part. Base measurement will be given on the drawing or blueprint, or it may be obtained from the
original part.
• Setback (SB)—is the distance from the bend tangent line to the mold point. In a 90-degree bend, SB = R + T (radius of the bend plus thickness of the metal). The setback dimension must be determined prior to making the bend because setback is used to determine the location of the beginning bend tangent line.
• Radius (R)—of the bend is always to the inside of the metal being formed unless otherwise stated. The minimum allowable radius for bending a given type and thickness of material should always be determined before proceeding with any bend allowance calculations.
• Mold line—is the line formed by extending the outside surfaces of the leg and the flange. (An imaginary point from which real base measurements are provided on drawings.)
• Bend tangent line—is the line at which the metal starts to bend and the line at which the metal stops curving. All the space between the bend tangent lines is the bend allowance.
• K number—is one of 179 numbers on the K chart that corresponds to one of the angles between 0 and 180 degrees to which metal can be bent. When metal is to be bent to any angle other than 90 degrees (K number of 1.0), the corresponding K number is selected from the chart and multiplied by the sum of the radius and the thickness of the metal. The product is the amount of setback for the bend.
• Closed angle—is less than 90 degrees when measured between legs. When the closed angle is 45 degrees, the amount of bend is 180 minus 45 or 135 degrees.
• Open angle—is more than 90 degrees when measured between legs or less than 90 degrees when the amount of bend is measured.
Bend Allowance Formula
By experimentation with actual bends in metals, aircraft engineers have found that accurate bending results could be obtained by using the following formula for any degree of bend from 1 to 180:
(0.0173 x R + 0.0078 x T) x N = BA
where
R = the desired bend radius,
T = the thickness of the material, and
N = the number of degrees of bend.
Refer to the General Manual for Structural Repair, Naval Air Systems Command (NAVAIR) manual 01-1A-1, for the appropriate bend allowance tables.
SHEET METAL SIZES
The thickness of sheet metal is usually specified by the non-linear measure known as its gauge. Thick sheet metal gauge sizes have low gauge numbers, while thinner sheet metal gauge numbers are high. Steel sheet metal sizes from 30 gauge to about 7 gauge are the most commonly used gauges. Gauge differs between iron based metals and non-iron based metals such as copper and aluminum.
There are many different metals that can be made into sheet metal, such as aluminum, brass, copper, steel, tin, nickel, and titanium. For decorative uses, important sheet metals include silver, gold, and platinum (platinum sheet metal is also utilized as a catalyst.)
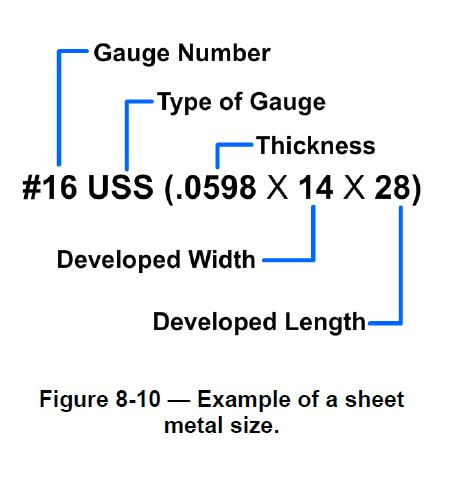
Metal thicknesses up to 0.25 inch (6 millimeters) are usually designated by a series of gauge numbers. Metal 0.25 inch and over is given in inch and millimeter sizes. In calling for the material size of sheet metal developments, it is customary to give the gauge number, type of gauge, and its inch or millimeter equivalent in brackets followed by the developed width and length in one sheet metal size (Figure 8-10). A gauge system is used for carbon steels but not appropriate for stainless steels where thickness is specified in decimals. The USS in Figure 8-10 identifies the type of gauge system, in this case the United States Standard gauge system.
• Closed angle—is less than 90 degrees when measured between legs. When the closed angle is 45 degrees, the amount of bend is 180 minus 45 or 135 degrees.
• Open angle—is more than 90 degrees when measured between legs or less than 90 degrees when the amount of bend is measured.
Bend Allowance Formula
By experimentation with actual bends in metals, aircraft engineers have found that accurate bending results could be obtained by using the following formula for any degree of bend from 1 to 180:
(0.0173 x R + 0.0078 x T) x N = BA
where
R = the desired bend radius,
T = the thickness of the material, and
N = the number of degrees of bend.
Refer to the General Manual for Structural Repair, Naval Air Systems Command (NAVAIR) manual 01-1A-1, for the appropriate bend allowance tables.
SHEET METAL SIZES
The thickness of sheet metal is usually specified by the non-linear measure known as its gauge. Thick sheet metal gauge sizes have low gauge numbers, while thinner sheet metal gauge numbers are high. Steel sheet metal sizes from 30 gauge to about 7 gauge are the most commonly used gauges. Gauge differs between iron based metals and non-iron based metals such as copper and aluminum.
There are many different metals that can be made into sheet metal, such as aluminum, brass, copper, steel, tin, nickel, and titanium. For decorative uses, important sheet metals include silver, gold, and platinum (platinum sheet metal is also utilized as a catalyst.)
Metal thicknesses up to 0.25 inch (6 millimeters) are usually designated by a series of gauge numbers. Metal 0.25 inch and over is given in inch and millimeter sizes. In calling for the material size of sheet metal developments, it is customary to give the gauge number, type of gauge, and its inch or millimeter equivalent in brackets followed by the developed width and length in one sheet metal size (Figure 8-10). A gauge system is used for carbon steels but not appropriate for stainless steels where thickness is specified in decimals. The USS in Figure 8-10 identifies the type of gauge system, in this case the United States Standard gauge system.
TYPES OF DEVELOPMENT
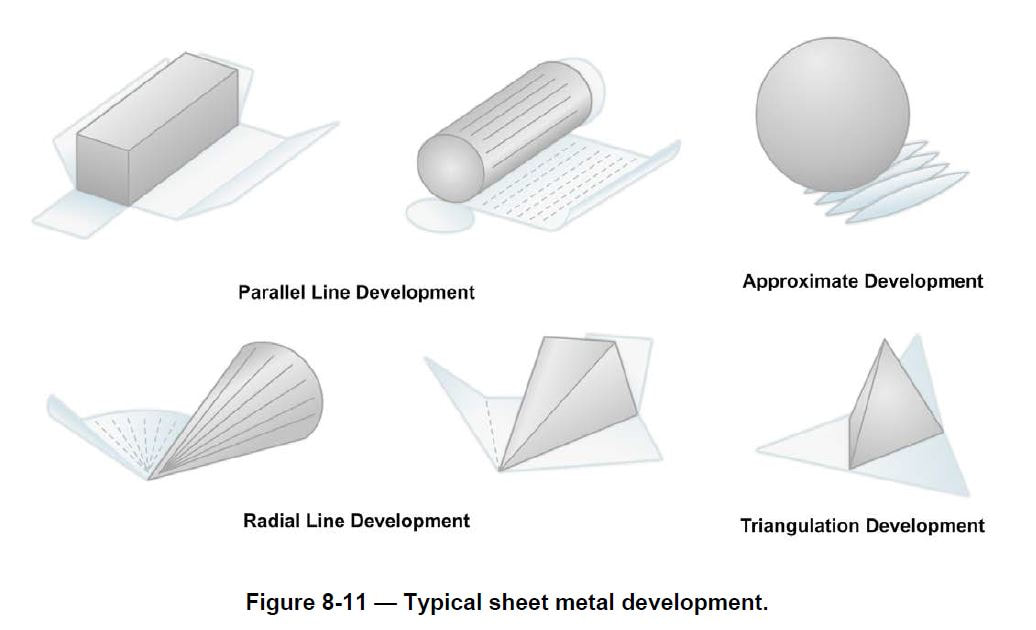
A surface is said to be develop-able if a thin sheet of flexible material, such as paper, can be wrapped smoothly about its surface. Therefore, objects that have plane, flat, or single-curved surfaces are develop-able. But a surface that is double-curved or warped is not considered develop-able, and approximate methods must be used to develop it. Typical sheet metal developments are illustrated in Figure 8-11.
A spherical shape would be an example of an approximate development. The material would be stretched to compensate for small inaccuracies. For example, the coverings for a football or basketball are made in segments. Each segment is cut to an approximate developed shape, and the segments are then stretched and sewed together to give the desired shape.
The three procedures commonly used in developing patterns are parallel-line, radial-line, and triangular development.
Parallel-parallel-line, radial-line, and triangular development.
A surface is said to be develop-able if a thin sheet of flexible material, such as paper, can be wrapped smoothly about its surface. Therefore, objects that have plane, flat, or single-curved surfaces are develop-able. But a surface that is double-curved or warped is not considered develop-able, and approximate methods must be used to develop it. Typical sheet metal developments are illustrated in Figure 8-11.
A spherical shape would be an example of an approximate development. The material would be stretched to compensate for small inaccuracies. For example, the coverings for a football or basketball are made in segments. Each segment is cut to an approximate developed shape, and the segments are then stretched and sewed together to give the desired shape.
The three procedures commonly used in developing patterns are parallel-line, radial-line, and triangular development.
Parallel-parallel-line, radial-line, and triangular development.
Parallel-Line Development
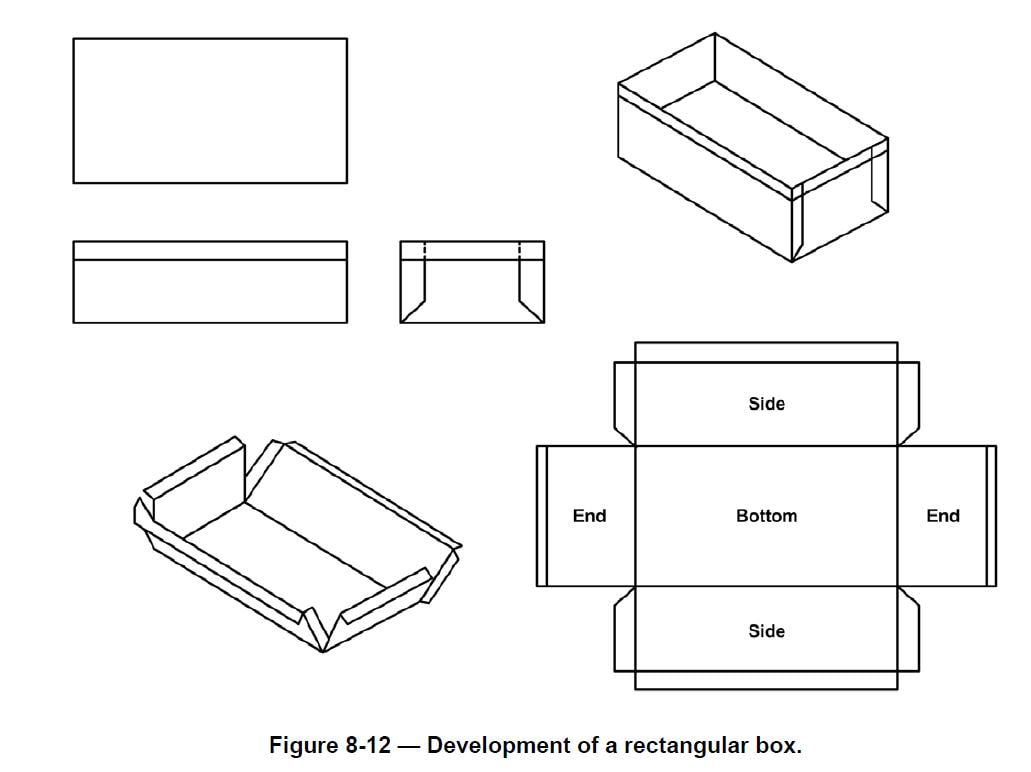
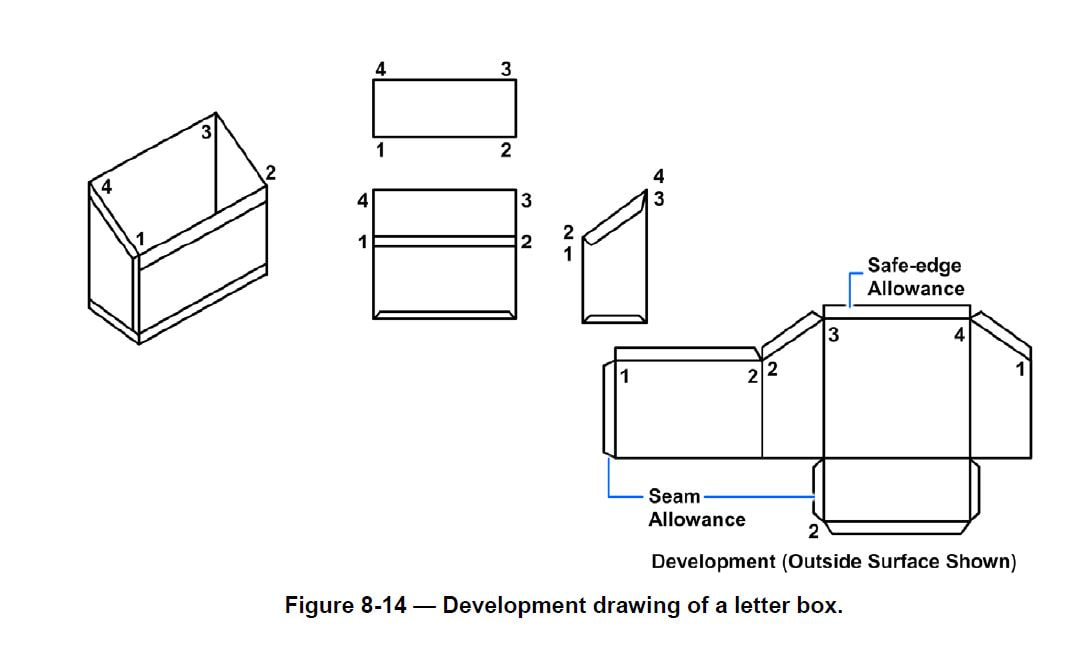
Parallel-line development refers to the development of an object that has surfaces on a flat plane of projection. The true size of each side of the object is known and the sides can be laid out in successive order. The development of a simple rectangular box with a bottom and four sides is illustrated in Figure 8-12. There is an allowance for lap seams at the corners and for a folded edge. The fold lines are shown as thin unbroken lines. Note that all lines for each surface are straight.
Parallel-line development refers to the development of an object that has surfaces on a flat plane of projection. The true size of each side of the object is known and the sides can be laid out in successive order. The development of a simple rectangular box with a bottom and four sides is illustrated in Figure 8-12. There is an allowance for lap seams at the corners and for a folded edge. The fold lines are shown as thin unbroken lines. Note that all lines for each surface are straight.
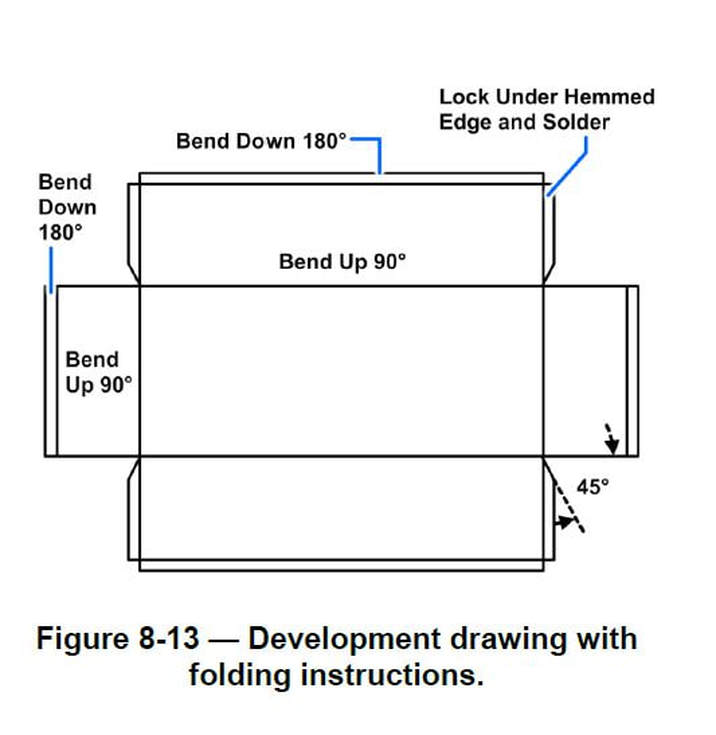
A parallel-line development drawing may include a complete set of folding instructions as shown in Figure 8-13. A letter box development drawing (Figure 8-14) illustrates that the back is higher than the front surface.
Parallel-line development is based upon the fact that a line that is parallel to another line is an equal distance from that line at all points. Objects that have opposite lines parallel to each other or that have the same cross-sectional shape throughout their length are developed by this method.
Parallel-line development is based upon the fact that a line that is parallel to another line is an equal distance from that line at all points. Objects that have opposite lines parallel to each other or that have the same cross-sectional shape throughout their length are developed by this method.
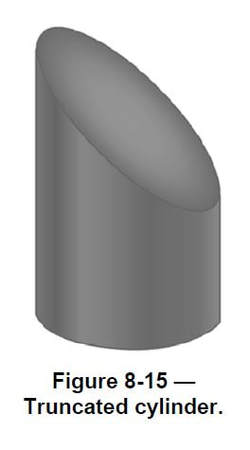
Truncated Cylinder
To gain a clear understanding of the parallel-line method, we will develop a layout of a truncated cylinder (Figure 8-15). Such a piece can be used as one half of a two-piece 90-degree elbow.
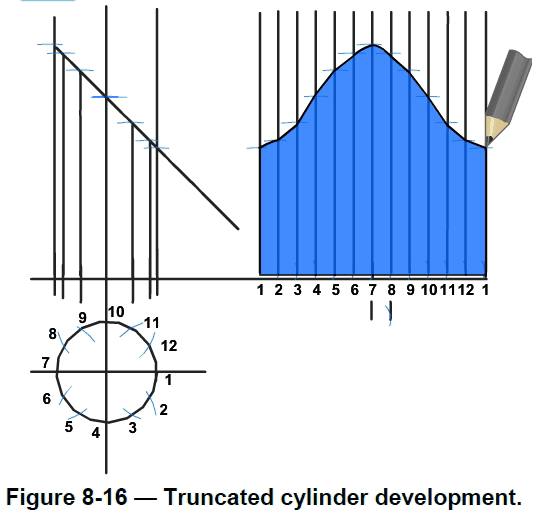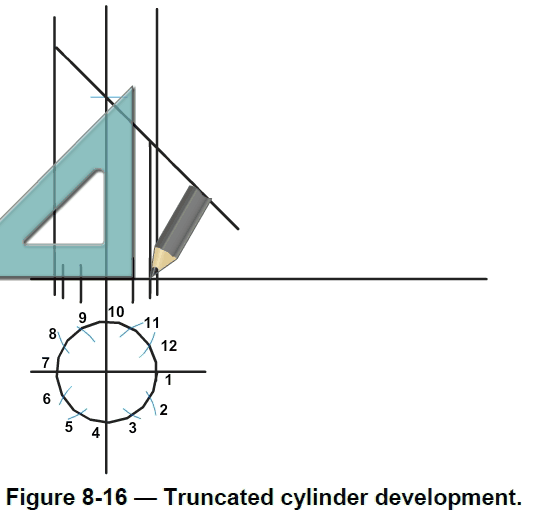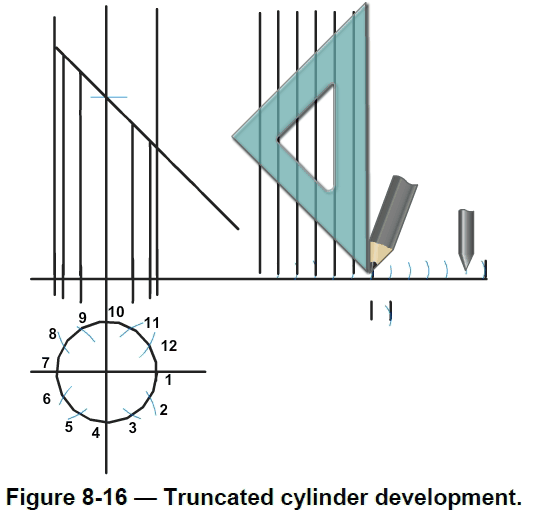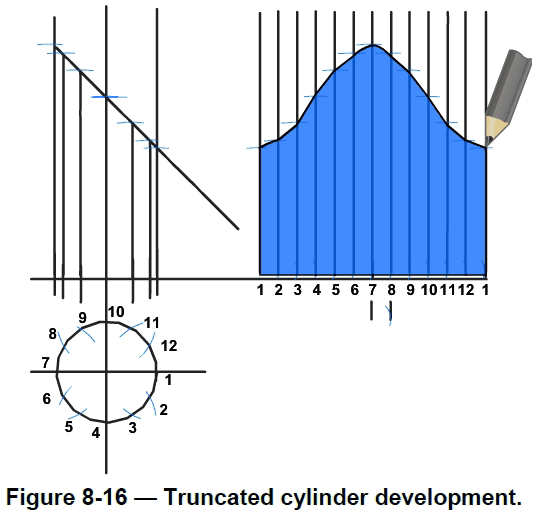
A truncated cylinder is developed in Figure 8-16:
1.Mark out reference lines using a set square.
2.Identify the diameter measurement and draw a circle. Here the diameter is 1 1/2 inches (40 millimeters).
3.Use the radius of the circle to divide the circumference into 12 equal sectors.
4.Label the marks 1 to 12. Note the numbers begin on the right-hand side and go in a clockwise direction.
5.Identify and mark the height of the cylinder. Here the height is 2 1/2 inches (60 millimeters).
6.Determine the angle of the top of the cylinder and use a setsquare.Here the angle is 45 degrees.
7.Mark off the radius on both sides of the reference line to construct the sides of the cylinder. Transfer numbers 1 to 12 from the circle to the base of the cylinder. Project these points to the top of the
cylinder.
8.Calculate the circumference of the cylinder to determine the stretch out length of the pattern. Use the formula C = πD. The diameter here is 1 1/2 inches (40 millimeters). Mark out the circumference on the horizontal base line.
To gain a clear understanding of the parallel-line method, we will develop a layout of a truncated cylinder (Figure 8-15). Such a piece can be used as one half of a two-piece 90-degree elbow.
A truncated cylinder is developed in Figure 8-16:
1.Mark out reference lines using a set square.
2.Identify the diameter measurement and draw a circle. Here the diameter is 1 1/2 inches (40 millimeters).
3.Use the radius of the circle to divide the circumference into 12 equal sectors.
4.Label the marks 1 to 12. Note the numbers begin on the right-hand side and go in a clockwise direction.
5.Identify and mark the height of the cylinder. Here the height is 2 1/2 inches (60 millimeters).
6.Determine the angle of the top of the cylinder and use a setsquare.Here the angle is 45 degrees.
7.Mark off the radius on both sides of the reference line to construct the sides of the cylinder. Transfer numbers 1 to 12 from the circle to the base of the cylinder. Project these points to the top of the
cylinder.
8.Calculate the circumference of the cylinder to determine the stretch out length of the pattern. Use the formula C = πD. The diameter here is 1 1/2 inches (40 millimeters). Mark out the circumference on the horizontal base line.
9.Divide the length of the circumference into 12. Draw a reference line and mark on it one-twelfth of the circumference.Use this measurement to set the dividers. Splitting the circumference into halves and quarters reduces tolerance error.
10.Use the dividers to mark the circumference into 12 equal divisions on the base line. Mark these divisions 1 to12. The final division is numbered 1.Project these divisions upward at 90 degrees.
11.Now develop the stretch out pattern.Transfer the length of the lines on the side view to the corresponding lines on the stretch out. Draw the top line curve of the pattern freehand, by using material like packing cord bent to the curve or by using a flexible curve.
12.This final shape is the stretch out pattern of the cylindrical shape and can be cut to shape to use as a template.
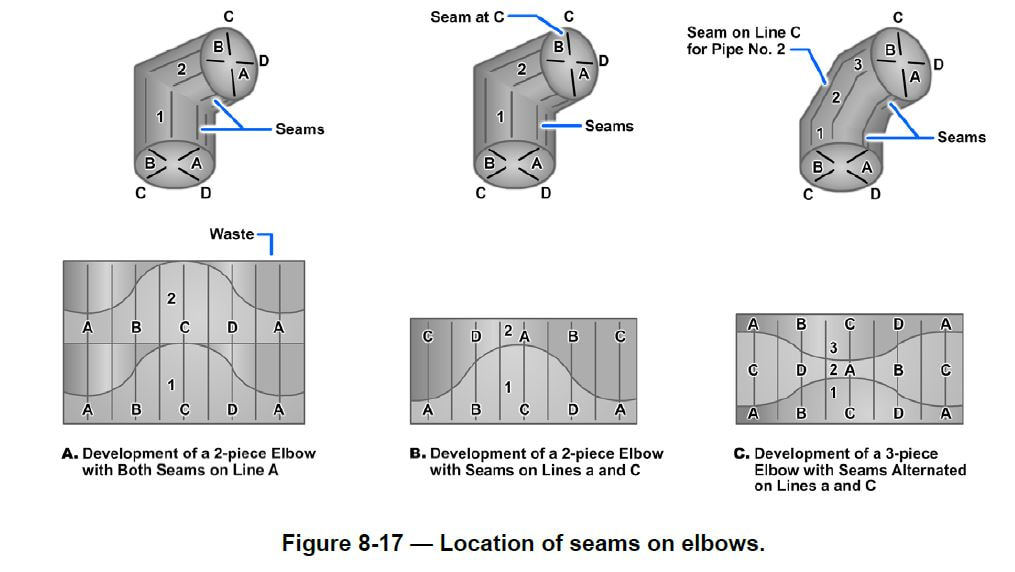
When the development is finished, the machinist will cut out the pattern. It is normal practice in sheet metal work to place the seam on the shortest side. However, in the development of elbows, the practice would result in considerable waste of material, as shown in Figure 8-17, view A. To avoid the waste and to simplify cutting the pieces, the seams are alternately placed 180 degrees apart, as shown in Figure 8-17, view B for a two-piece elbow, and view C for a three-piece elbow.
10.Use the dividers to mark the circumference into 12 equal divisions on the base line. Mark these divisions 1 to12. The final division is numbered 1.Project these divisions upward at 90 degrees.
11.Now develop the stretch out pattern.Transfer the length of the lines on the side view to the corresponding lines on the stretch out. Draw the top line curve of the pattern freehand, by using material like packing cord bent to the curve or by using a flexible curve.
12.This final shape is the stretch out pattern of the cylindrical shape and can be cut to shape to use as a template.
When the development is finished, the machinist will cut out the pattern. It is normal practice in sheet metal work to place the seam on the shortest side. However, in the development of elbows, the practice would result in considerable waste of material, as shown in Figure 8-17, view A. To avoid the waste and to simplify cutting the pieces, the seams are alternately placed 180 degrees apart, as shown in Figure 8-17, view B for a two-piece elbow, and view C for a three-piece elbow.
Radial-Line Development
In radial-line development, the slanting lines of pyramids and cones do not always appear in their true lengths in an orthographic view; the designer must find other means to depict them.
The radial-line method is similar in some respects to the parallel-line method. Evenly spaced reference lines are necessary in both of these methods. However, in parallel-line development, the reference lines are parallel—like a picket fence. In radial-line development, the reference lines radiate from the apex of a cone—like the spokes of a wheel.
The reference lines in parallel-line development project horizontally. In radial-line development, the reference lines are transferred from the front view to the development with the dividers.
Developing a pattern for the frustum of a right cone is a typical practice project that will help you get the feel of the radial-line method. You are familiar with the shape of a cone. A right cone is one that, if set flat side down on a flat surface, would stand straight up. In other words, a centerline drawn from the point, or vertex, to the base line would form a right angle with that line. The frustum of a cone is that part that remains after the point, or top, has been removed.
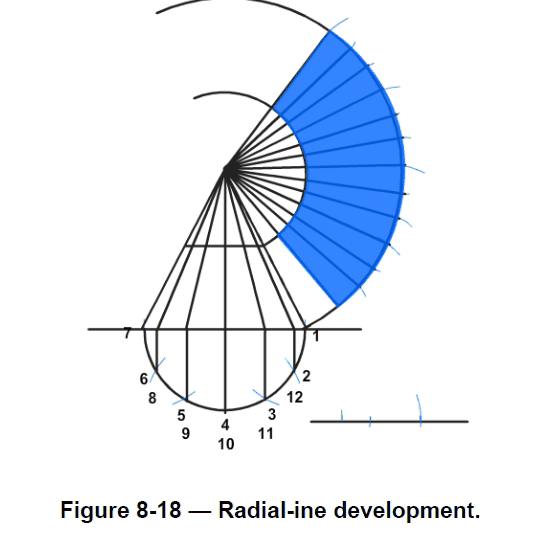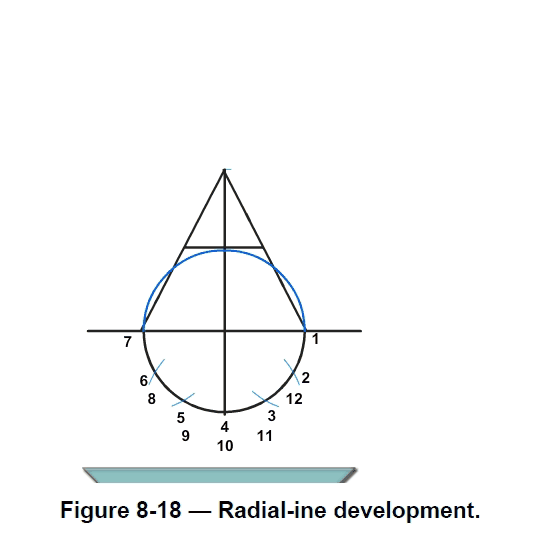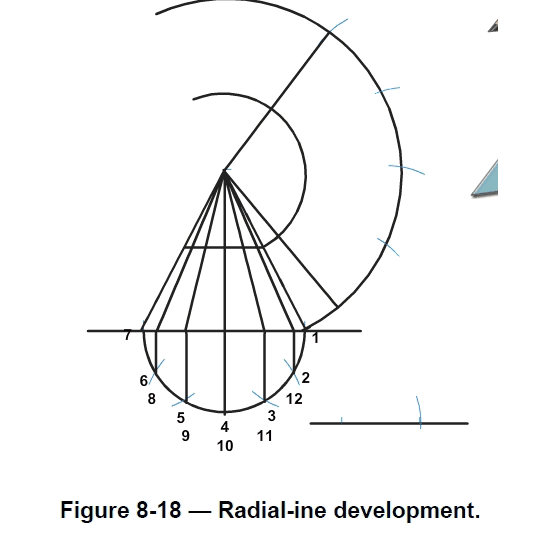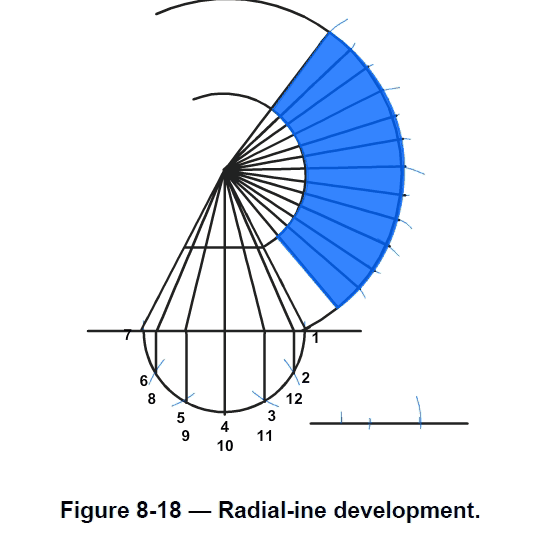
The procedure for developing a frustum of a right cone is given below. Check each step of the procedure against the development shown in Figure 8-18.
1.First establish the apex point (H).
2.Draw reference lines using a set square. Mark out the measurements of the:
a.Base (D) – 2 3/4 inches (70 millimeters).
b.Apex (H) – 4 inches (100 millimeters).
c.Frustum height (h) – 2 inches (50 millimeters).
3.Draw in the reference lines from the apex (H) to the base (D). Check that the frustum diameter (d) is 1 3/8 inches (35 millimeters).
4.Develop the half circle representing half the bottom view.
5.Set the dividers at 1 3/8 inches (35 millimeters) - the radius of the base of the frustum (D). Divide the half circle into 6 equal sectors.
6.Label the marks 1 to 12 as indicated.
7.Project each of the sectors up to the base line at 90 degrees. Project these lines to the apex.
8.Develop the stretch out pattern of the frustum. Place the compass point on the apex. Set theradius to A and swing an arc as indicated. Repeat with the radius set to B.
9.Draw a line from the apex to the bottom circumference, away from the base of the frustum.The intersection point will be the start for marking out the base circumference into 12 sectors.
In radial-line development, the slanting lines of pyramids and cones do not always appear in their true lengths in an orthographic view; the designer must find other means to depict them.
The radial-line method is similar in some respects to the parallel-line method. Evenly spaced reference lines are necessary in both of these methods. However, in parallel-line development, the reference lines are parallel—like a picket fence. In radial-line development, the reference lines radiate from the apex of a cone—like the spokes of a wheel.
The reference lines in parallel-line development project horizontally. In radial-line development, the reference lines are transferred from the front view to the development with the dividers.
Developing a pattern for the frustum of a right cone is a typical practice project that will help you get the feel of the radial-line method. You are familiar with the shape of a cone. A right cone is one that, if set flat side down on a flat surface, would stand straight up. In other words, a centerline drawn from the point, or vertex, to the base line would form a right angle with that line. The frustum of a cone is that part that remains after the point, or top, has been removed.
The procedure for developing a frustum of a right cone is given below. Check each step of the procedure against the development shown in Figure 8-18.
1.First establish the apex point (H).
2.Draw reference lines using a set square. Mark out the measurements of the:
a.Base (D) – 2 3/4 inches (70 millimeters).
b.Apex (H) – 4 inches (100 millimeters).
c.Frustum height (h) – 2 inches (50 millimeters).
3.Draw in the reference lines from the apex (H) to the base (D). Check that the frustum diameter (d) is 1 3/8 inches (35 millimeters).
4.Develop the half circle representing half the bottom view.
5.Set the dividers at 1 3/8 inches (35 millimeters) - the radius of the base of the frustum (D). Divide the half circle into 6 equal sectors.
6.Label the marks 1 to 12 as indicated.
7.Project each of the sectors up to the base line at 90 degrees. Project these lines to the apex.
8.Develop the stretch out pattern of the frustum. Place the compass point on the apex. Set theradius to A and swing an arc as indicated. Repeat with the radius set to B.
9.Draw a line from the apex to the bottom circumference, away from the base of the frustum.The intersection point will be the start for marking out the base circumference into 12 sectors.
10.The frustum circumference is D = 3.14 x 2 3/4 inches = 8 43/64 inches (220 millimeters). Mark the base circumference into 12 equal sectors. Calculate the length of each sector:
= 8 4364 𝑖𝑖𝑖𝑖𝑖𝑖ℎ𝑒𝑒𝑒𝑒 (220 𝑚𝑚𝑚 𝑚𝑚𝑚𝑚𝑚 𝑚𝑚𝑚 𝑚𝑚𝑚 𝑚𝑚𝑚 )/12 = 0.72 𝑖𝑖𝑖𝑖𝑖𝑖ℎ𝑒𝑒𝑒𝑒 (18.3 𝑚𝑚𝑚 𝑚𝑚𝑚𝑚𝑚 𝑚𝑚𝑚 𝑚𝑚𝑚 𝑚𝑚𝑚 )
11.Draw a reference line and mark out 23/32 inch (18.3 millimeters). Set the dividers to this distance. Mark off the 12 divisions along the circumference.
12.Project each of these to the apex to form the radial lines. The radial lines will be used in theforming process. The shape shaded in blue is the radial-line stretch out pattern for the rightcone frustum.
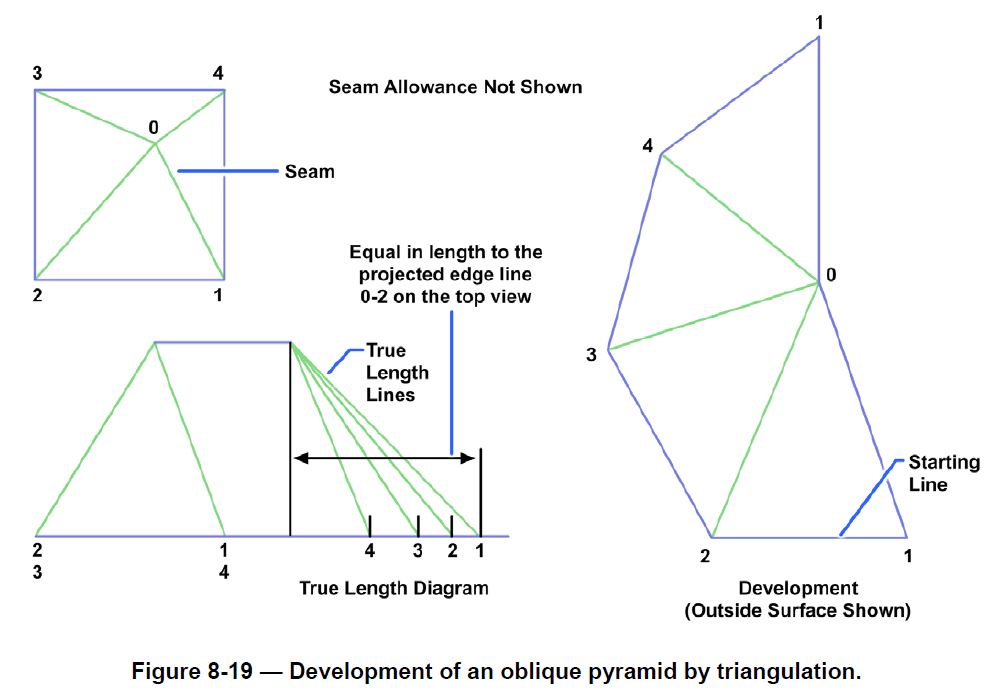
Oblique Pyramid
The oblique pyramid in Figure 8-19 has all its lateral edges of unequal length. The true length of each of these edges must first be found as shown in the true-length diagram. The development may now be constructed as follows:
= 8 4364 𝑖𝑖𝑖𝑖𝑖𝑖ℎ𝑒𝑒𝑒𝑒 (220 𝑚𝑚𝑚 𝑚𝑚𝑚𝑚𝑚 𝑚𝑚𝑚 𝑚𝑚𝑚 𝑚𝑚𝑚 )/12 = 0.72 𝑖𝑖𝑖𝑖𝑖𝑖ℎ𝑒𝑒𝑒𝑒 (18.3 𝑚𝑚𝑚 𝑚𝑚𝑚𝑚𝑚 𝑚𝑚𝑚 𝑚𝑚𝑚 𝑚𝑚𝑚 )
11.Draw a reference line and mark out 23/32 inch (18.3 millimeters). Set the dividers to this distance. Mark off the 12 divisions along the circumference.
12.Project each of these to the apex to form the radial lines. The radial lines will be used in theforming process. The shape shaded in blue is the radial-line stretch out pattern for the rightcone frustum.
Oblique Pyramid
The oblique pyramid in Figure 8-19 has all its lateral edges of unequal length. The true length of each of these edges must first be found as shown in the true-length diagram. The development may now be constructed as follows:
1.Lay out base line 1-2 in the development view equal in length to base line 1-2 found in the topview.
2.With point 1 as center and a radius equal in length to line 0-1 in the true diagram, swing an arc.
3.With point 2 as center and a radius equal in length to line 0-2 in the true-length diagram, swingan arc intersecting the first arc at 0.
4.With point 0 as center and a radius equal in length to line 0-3 in the true-length diagram, swingan arc.
5.With point 2 as center and radius equal in length to base line 2-3 found in the top view, swingan arc intersecting the first arc at point 3.
6.Locate points 4 and 1 in a similar manner, and join those points, as shown, with straight lines.
The base and seam lines have been omitted on the development drawing.
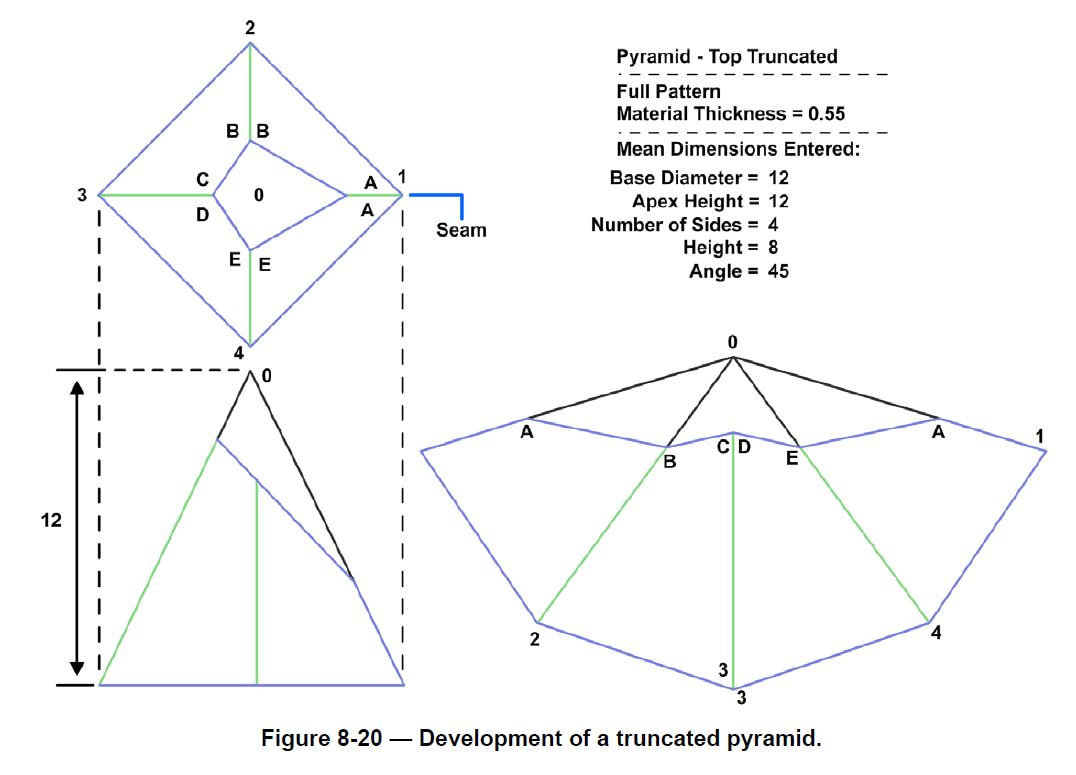
Truncated Pyramid
The truncated pyramid in Figure 8-20 has all its lateral edges of unequal length. The true length of each of these edges must first be found. The procedure for developing a truncated pyramid is given below. Check each step of the procedure against the development shown in Figure 8-20.
1.First draw the orthographic views of the truncated pyramid.
2.Identify the base diameter. Here the base diameter is 12 inches.
3.Identify and mark the height of the apex. Here the height is 12 inches.
4.Identify and mark the height of the truncated pyramid. Here the height is 8 inches.
5.Determine the angle of the top of the truncated pyramid and use a setsquare. Here the angle is45 degrees.
2.With point 1 as center and a radius equal in length to line 0-1 in the true diagram, swing an arc.
3.With point 2 as center and a radius equal in length to line 0-2 in the true-length diagram, swingan arc intersecting the first arc at 0.
4.With point 0 as center and a radius equal in length to line 0-3 in the true-length diagram, swingan arc.
5.With point 2 as center and radius equal in length to base line 2-3 found in the top view, swingan arc intersecting the first arc at point 3.
6.Locate points 4 and 1 in a similar manner, and join those points, as shown, with straight lines.
The base and seam lines have been omitted on the development drawing.
Truncated Pyramid
The truncated pyramid in Figure 8-20 has all its lateral edges of unequal length. The true length of each of these edges must first be found. The procedure for developing a truncated pyramid is given below. Check each step of the procedure against the development shown in Figure 8-20.
1.First draw the orthographic views of the truncated pyramid.
2.Identify the base diameter. Here the base diameter is 12 inches.
3.Identify and mark the height of the apex. Here the height is 12 inches.
4.Identify and mark the height of the truncated pyramid. Here the height is 8 inches.
5.Determine the angle of the top of the truncated pyramid and use a setsquare. Here the angle is45 degrees.
6.Mark off the radius on both sides of the reference line to construct the sides of the truncated pyramid.
7.The intersecting points establish the true length of all segments.
8.Now develop the stretch out pattern. Transfer the length of the lines on the side view to the corresponding lines on the stretch out view.
9.The final shape is the stretch out pattern of the cylindrical shape and can be cut to shape to use as a template.
Triangular Development
Triangulation is slower and more difficult than parallel-line or radial-line development, but it is more practical for many types of figures. Additionally, it is the only method by which the development of warped surfaces may be estimated. In development by triangulation, the piece is divided into a series of triangles, as in radial-line development. However, there is no one single apex for the triangles. The problem becomes one of finding the true lengths of the varying oblique lines. Drawing a true-length diagram solves the problem.
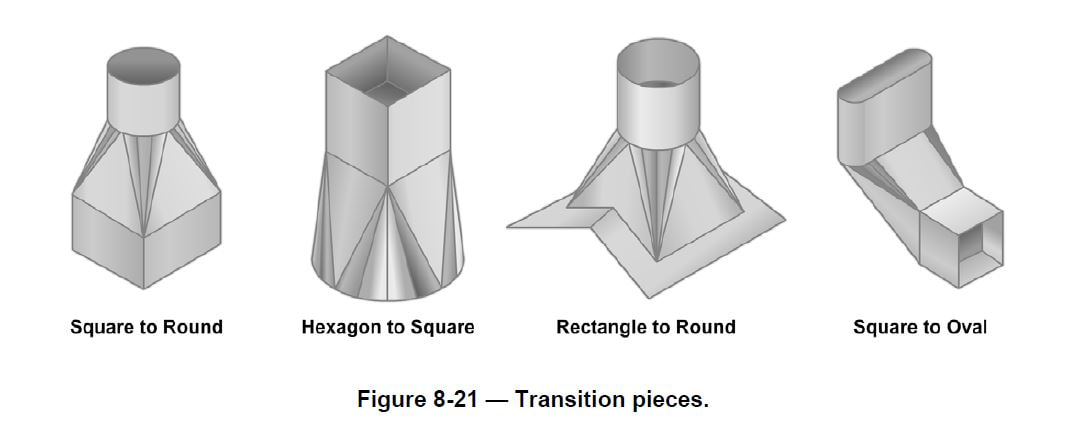
An example of a layout using triangulation is the development of a transition piece (Figure 8-21). Transition pieces are usually made to connect two different shapes of pipes, such as square to round, rectangular to round, and hexagonal to round. Transition pieces can be used to form parallel and oblique joints where the piping may not be perpendicular to the pipe axis. These transition pieces will usually fit the definition of a non-develop-able surface that must be developed by approximation.
7.The intersecting points establish the true length of all segments.
8.Now develop the stretch out pattern. Transfer the length of the lines on the side view to the corresponding lines on the stretch out view.
9.The final shape is the stretch out pattern of the cylindrical shape and can be cut to shape to use as a template.
Triangular Development
Triangulation is slower and more difficult than parallel-line or radial-line development, but it is more practical for many types of figures. Additionally, it is the only method by which the development of warped surfaces may be estimated. In development by triangulation, the piece is divided into a series of triangles, as in radial-line development. However, there is no one single apex for the triangles. The problem becomes one of finding the true lengths of the varying oblique lines. Drawing a true-length diagram solves the problem.
An example of a layout using triangulation is the development of a transition piece (Figure 8-21). Transition pieces are usually made to connect two different shapes of pipes, such as square to round, rectangular to round, and hexagonal to round. Transition pieces can be used to form parallel and oblique joints where the piping may not be perpendicular to the pipe axis. These transition pieces will usually fit the definition of a non-develop-able surface that must be developed by approximation.
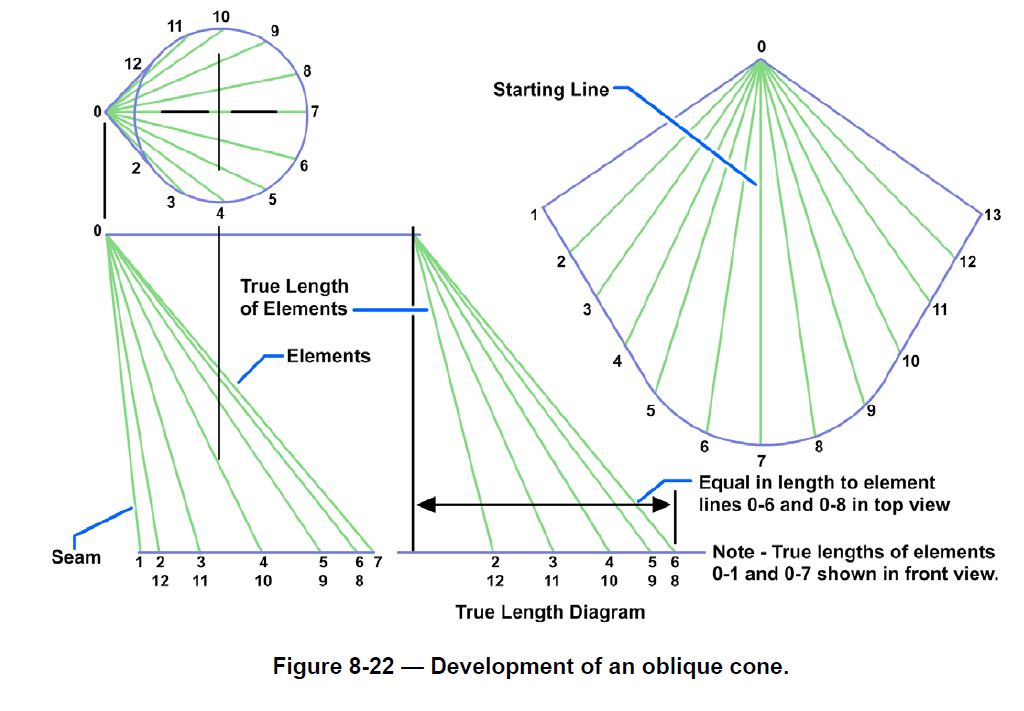
Oblique Cone
An oblique cone is generally developed by the triangulation method.
The base of the cone is divided into an equal number of divisions. The elements 0-1, 0-2, and so on are drawn in the top view, projected down, and drawn in the front view. The true lengths of the elements are not shown in either the top or front view, but would be equal in length to the hypotenuse of a right triangle, having one leg equal in length to the projected element in the top view and the other leg equal to the height of the projected element in the front view. When it is necessary to find the true length of a number of edges, or elements, then a true-length diagram can be drawn adjacent to the front view, preventing the front view from being cluttered with lines.
Since the development of the oblique cone (Figure 8-22) will be symmetrical, the starting line will be element 0-13. The development is constructed as follows:
1.With 0 as center and the radius equal to the true length of element 0-12, draw an arc.
2.With 13 as center and the radius equal to distance 12-13 in the top view, draw a second arcintersecting the first point at 12. Draw element 0-12 on the development.
3.With 0 as center and the radius equal to the true length of element 0-11, draw an arc. With 11as center and the radius equal to distance 11-12 in the top view, draw a second arc intersecting the first point at 11. Draw element 0-11 on the development.
4.Repeat these steps with the remaining elements until all element lines are located on the development view.
An oblique cone is generally developed by the triangulation method.
The base of the cone is divided into an equal number of divisions. The elements 0-1, 0-2, and so on are drawn in the top view, projected down, and drawn in the front view. The true lengths of the elements are not shown in either the top or front view, but would be equal in length to the hypotenuse of a right triangle, having one leg equal in length to the projected element in the top view and the other leg equal to the height of the projected element in the front view. When it is necessary to find the true length of a number of edges, or elements, then a true-length diagram can be drawn adjacent to the front view, preventing the front view from being cluttered with lines.
Since the development of the oblique cone (Figure 8-22) will be symmetrical, the starting line will be element 0-13. The development is constructed as follows:
1.With 0 as center and the radius equal to the true length of element 0-12, draw an arc.
2.With 13 as center and the radius equal to distance 12-13 in the top view, draw a second arcintersecting the first point at 12. Draw element 0-12 on the development.
3.With 0 as center and the radius equal to the true length of element 0-11, draw an arc. With 11as center and the radius equal to distance 11-12 in the top view, draw a second arc intersecting the first point at 11. Draw element 0-11 on the development.
4.Repeat these steps with the remaining elements until all element lines are located on the development view.
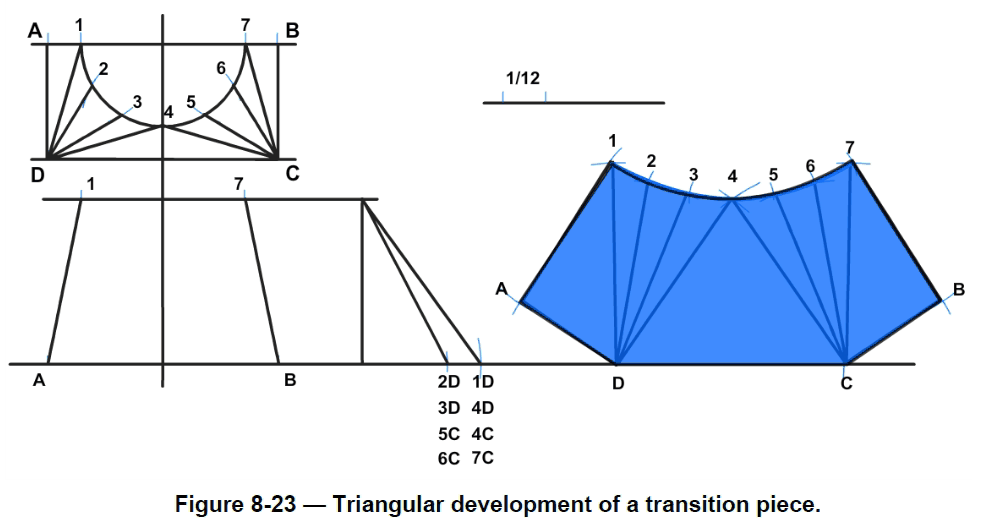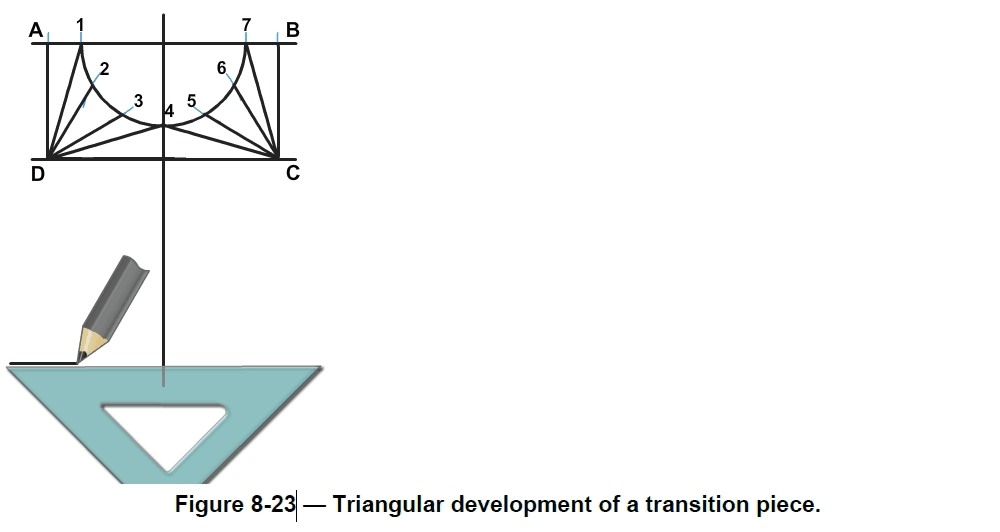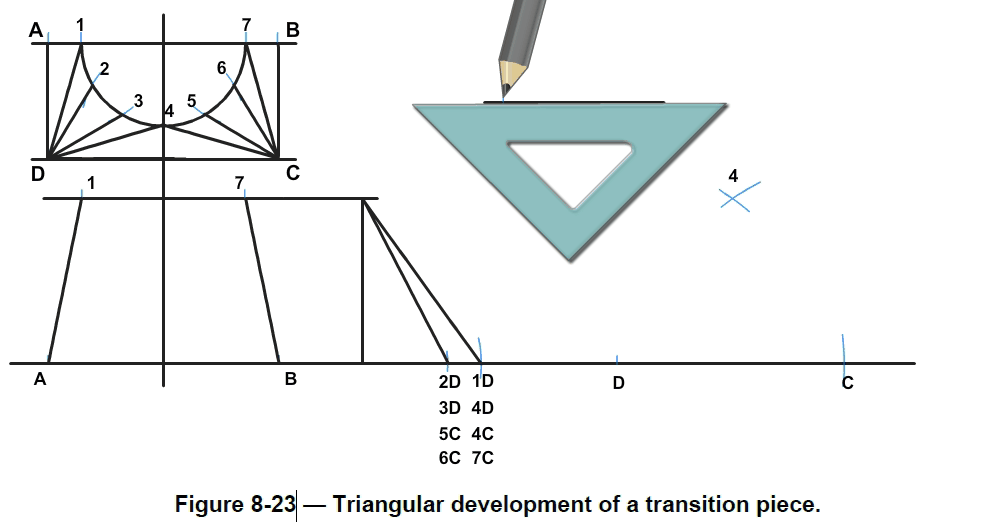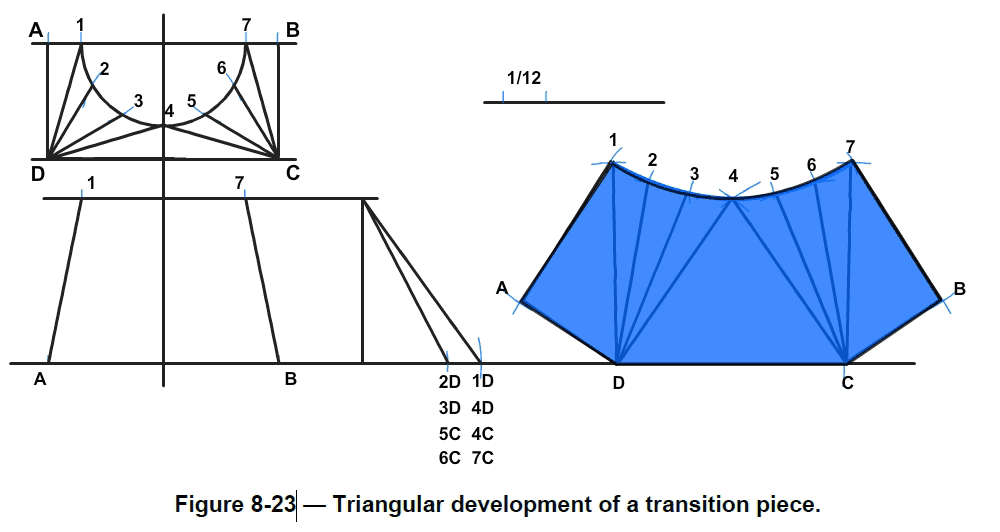
Square-to-Round
The steps in the triangulation of a warped transition piece joining a large, square duct and a small, round duct are shown in Figure 8-23. The steps are as follows:
1.First establish the reference lines.
2.Develop the top view. With a set square, mark out the measurements for half the base, andlabel each corner (from the top left-hand corner, moving clockwise) A to D.
3.From the center of the half base, draw a semicircle with radius 1 inch (25 millimeter). Checkthat the diameter (D) is 2 inches (50 millimeters).
The steps in the triangulation of a warped transition piece joining a large, square duct and a small, round duct are shown in Figure 8-23. The steps are as follows:
1.First establish the reference lines.
2.Develop the top view. With a set square, mark out the measurements for half the base, andlabel each corner (from the top left-hand corner, moving clockwise) A to D.
3.From the center of the half base, draw a semicircle with radius 1 inch (25 millimeter). Checkthat the diameter (D) is 2 inches (50 millimeters).
4.Divide the half circle into six equal spaces by placing the compass point on the three pointswhere the semicircle intersects the reference lines and swinging small arcs (R = 1 inch (25millimeter)) to intersect the circle. Number the points 1 to 7 as shown.
5.Using a set square, draw lines from point D on the base of the shape to points 1 through to 4on the half circle. Next, draw lines from C on the base of the shape to points 4 through to 7,which completes (half) the top view.
6.Draw the side view. First, draw a reference line. Remember, the vertical height is 50millimeters, and the diameter of the top is 50 millimeters.
7.The base is 2 3/4 inches (70 millimeters) square. Draw lines from the base to the top. Label the base points A and B. Label the top points 1 and 7.
8.Now develop the stretch out pattern for the square-to-round. First establish a reference line(extending to the right from point B on the side view) for the base of the stretch out pattern.Draw the vertical height of the square-to-round somewhere to the right of the side view,perpendicular to the base line.
a.Now place the compass point on D in the top view. Set the radius to point 2 on the halfcircle. Place the compass point at the intersection of the base line and the vertical heightline and swing an arc to mark the base line. Label this point 2D. Note this point is theshortest distance from point D to the top of the half circle, the same length as 3D, 5C, and6C.
b.Now place the compass at D and set the radius to point 1 on the half circle. Transfer thecompass to the intersection of the base line and the vertical height line and swing an arc tomark the base line. Label the point 1D. Note this point is the longer distance from point D tothe top of the half diameter, the same length as 4D, 4C, and 7C.
c.Now draw a line from the top of the vertical height line to point 2D, and then from the top to point 1D. This diagram is called the true-length diagram.
9.Mark a point on the base line to the right of point 1D.
10.Set the compass at the distance between D and C on the top view (the true length), thentransfer the distance D to C to the base line. Label the points D and C. Reset the compass tothe length of the line 4D. Placing one point on D, draw an arc midway between D and C. Shiftthe compass to C, draw an arc to bisect the previous one. Label this point 4.
11.Mark out a new short reference line for one-twelfth of the circumference of the top of thesquare-to-round shape. Calculate the circumference of the top of the shape, and then divide itby 12.
C = πD
C = 3.14 x 2 inches (50 millimeters)
= 6 13/64 inches (157 millimeters) One-twelfth of the circle
= 6 13/64 inches (157 millimeters) ÷ 12 = 1/2 inch (13 millimeters)
12.Measure and mark out 1/2 inch (13 millimeters) on the reference line. Set the compass at 1/2 inch (13 millimeters) (one-twelfth circumference).
a.Place the compass on point 4, and swing arcs to mark to the right and to the left. Set thecompass at the true length of reference line 2D. Place the compass on point D, and swingan arc to intersect the arc on the left. Label this point 3. Place the compass on C, andswing an arc to intersect the arc on the right. Label this point 5.
b.Reset the compass at 1/2 inch (13 millimeters), using the measure on the reference line. Place the compass on point 5 and swing an arc to the right hand side. Swing an arc to the left of point 3.
c.Reset the compass at the length of the reference line 2D. Place the compass on point D,make a mark intersecting the arc, and label this point 2. Place the compass on C, make amark intersecting the arc, and label this point 6.
d.Repeat the process, swinging an arc R13 to the left of 2 and right of 6. This time, however,reset the compass to the length of reference line 1D. Place the compass point on D, makea mark intersecting the arc, and label this point 1. Place the compass on C and make amark intersecting the arc. Label this point 7.
13.Develop the half square base from point D to point A.
a.Using the side view diagram, set the compass at the distance between B and 7. Place thecompass at point 1 on the stretch out pattern, and draw an arc to the lower left. Repeat theprocess from point 7 to the lower right.
b.Reset the compass to the distance between B and C on the top view diagram. Place thecompass on D and make a mark intersecting the arc. Label this point A. Place the compasson C, make a mark intersecting the arc, and label this point B.
c.Using a set square or ruler, draw lines joining 1 and A; A and D; 7 and B; and B and C.Draw lines from D to 1, 2, 3, and 4. Draw lines from C to 4, 5, 6, and 7.
14.Use a flexible ruler, or freehand to join points 1 to 7.
This completes the stretch out half pattern for a square-to-round shape, using the triangulation method. This development does not show a seam allowance.
5.Using a set square, draw lines from point D on the base of the shape to points 1 through to 4on the half circle. Next, draw lines from C on the base of the shape to points 4 through to 7,which completes (half) the top view.
6.Draw the side view. First, draw a reference line. Remember, the vertical height is 50millimeters, and the diameter of the top is 50 millimeters.
7.The base is 2 3/4 inches (70 millimeters) square. Draw lines from the base to the top. Label the base points A and B. Label the top points 1 and 7.
8.Now develop the stretch out pattern for the square-to-round. First establish a reference line(extending to the right from point B on the side view) for the base of the stretch out pattern.Draw the vertical height of the square-to-round somewhere to the right of the side view,perpendicular to the base line.
a.Now place the compass point on D in the top view. Set the radius to point 2 on the halfcircle. Place the compass point at the intersection of the base line and the vertical heightline and swing an arc to mark the base line. Label this point 2D. Note this point is theshortest distance from point D to the top of the half circle, the same length as 3D, 5C, and6C.
b.Now place the compass at D and set the radius to point 1 on the half circle. Transfer thecompass to the intersection of the base line and the vertical height line and swing an arc tomark the base line. Label the point 1D. Note this point is the longer distance from point D tothe top of the half diameter, the same length as 4D, 4C, and 7C.
c.Now draw a line from the top of the vertical height line to point 2D, and then from the top to point 1D. This diagram is called the true-length diagram.
9.Mark a point on the base line to the right of point 1D.
10.Set the compass at the distance between D and C on the top view (the true length), thentransfer the distance D to C to the base line. Label the points D and C. Reset the compass tothe length of the line 4D. Placing one point on D, draw an arc midway between D and C. Shiftthe compass to C, draw an arc to bisect the previous one. Label this point 4.
11.Mark out a new short reference line for one-twelfth of the circumference of the top of thesquare-to-round shape. Calculate the circumference of the top of the shape, and then divide itby 12.
C = πD
C = 3.14 x 2 inches (50 millimeters)
= 6 13/64 inches (157 millimeters) One-twelfth of the circle
= 6 13/64 inches (157 millimeters) ÷ 12 = 1/2 inch (13 millimeters)
12.Measure and mark out 1/2 inch (13 millimeters) on the reference line. Set the compass at 1/2 inch (13 millimeters) (one-twelfth circumference).
a.Place the compass on point 4, and swing arcs to mark to the right and to the left. Set thecompass at the true length of reference line 2D. Place the compass on point D, and swingan arc to intersect the arc on the left. Label this point 3. Place the compass on C, andswing an arc to intersect the arc on the right. Label this point 5.
b.Reset the compass at 1/2 inch (13 millimeters), using the measure on the reference line. Place the compass on point 5 and swing an arc to the right hand side. Swing an arc to the left of point 3.
c.Reset the compass at the length of the reference line 2D. Place the compass on point D,make a mark intersecting the arc, and label this point 2. Place the compass on C, make amark intersecting the arc, and label this point 6.
d.Repeat the process, swinging an arc R13 to the left of 2 and right of 6. This time, however,reset the compass to the length of reference line 1D. Place the compass point on D, makea mark intersecting the arc, and label this point 1. Place the compass on C and make amark intersecting the arc. Label this point 7.
13.Develop the half square base from point D to point A.
a.Using the side view diagram, set the compass at the distance between B and 7. Place thecompass at point 1 on the stretch out pattern, and draw an arc to the lower left. Repeat theprocess from point 7 to the lower right.
b.Reset the compass to the distance between B and C on the top view diagram. Place thecompass on D and make a mark intersecting the arc. Label this point A. Place the compasson C, make a mark intersecting the arc, and label this point B.
c.Using a set square or ruler, draw lines joining 1 and A; A and D; 7 and B; and B and C.Draw lines from D to 1, 2, 3, and 4. Draw lines from C to 4, 5, 6, and 7.
14.Use a flexible ruler, or freehand to join points 1 to 7.
This completes the stretch out half pattern for a square-to-round shape, using the triangulation method. This development does not show a seam allowance.
Rectangular-to-Round
The transition piece shown in Figure 8-24 is constructed in the same manner as the square-to-round except that all the elements are of different lengths. To avoid confusion, four true-length diagrams are drawn and the true-length lines are clearly labeled.
The transition piece shown in Figure 8-24 is constructed in the same manner as the square-to-round except that all the elements are of different lengths. To avoid confusion, four true-length diagrams are drawn and the true-length lines are clearly labeled.
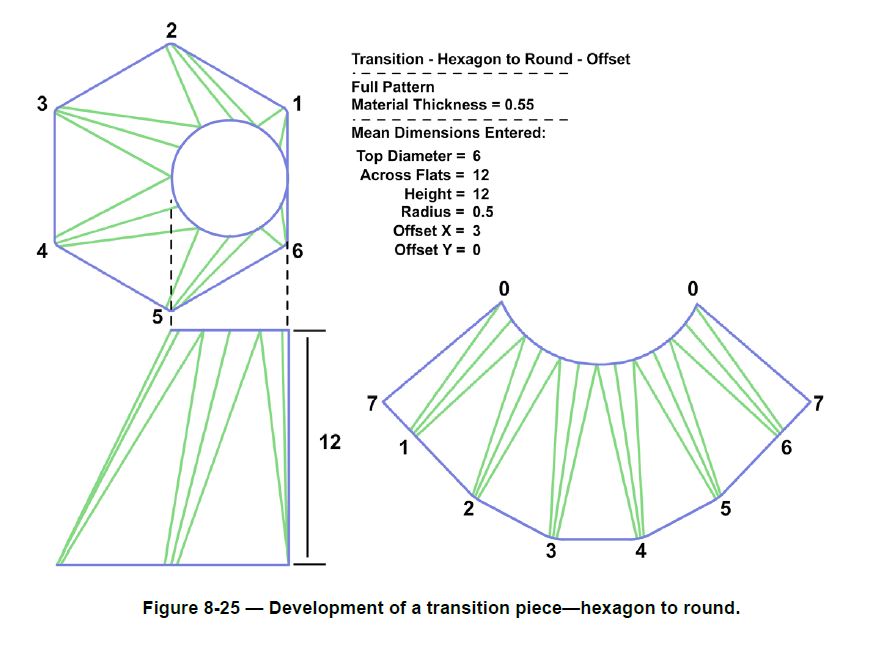
Hexagon-to-Round
The transition piece shown in Figure 8-25 is constructed in the same manner as the square-to-round and the rectangular-to-round transition pieces, as all of the elements are, once again, different lengths.
The transition piece shown in Figure 8-25 is constructed in the same manner as the square-to-round and the rectangular-to-round transition pieces, as all of the elements are, once again, different lengths.
Developments and Intersections
Review Questions
8-1 For which of the following reasons should the sheet metal development drawings allow additional material?
A. Compression during shaping
B. Damage to the material
C. Joining of edges
D. Miscalculations
8-2. When drawing a lap seam, the allowance must be how many times the diameter of the rivet being used?
A. 1
B. 3
C. 5
D. 7
8-3. If the finished part is not shown with the development, what item should be included?
A. A scale model
B. Drawing instructions
C. Color code list
D. Marking instructions
8-4. Which of the following terms describes the amount of material consumed in making a bend?
A. Base measurement
B. Bend allowance
C. Bend tangent line
D. Setback
8-5. The three procedures commonly used in developing patterns are parallel-line, radial-line, and what other type of development?
A. Circular
B. Perspective
C. Rectangular
D. Triangular
8-6. Which of the following statements defines parallel-line development?
A. The development of an object that has surfaces on a flat plane of projection
B. The development of an object that has surfaces on a slanting plane of projection
C. The first series of prints used in construction and manufacturing
D. The perspective print of the development of parallel roadways
8-7. The parallel-line development is based upon which of the following principles?
A. A line parallel to another line is an equal distance from that line at all points
B. A line perpendicular to another line will intersect at only one point
C. The lines radiate from the apex of a cone
D. When finished, the lines form a three-dimensional drawing
8-8. What type of development is used when an object has the same cross-sectional shape throughout the length?
A. Orthographic-perspective
B. Parallel-line
C. Radial-line
D. Triangular
8-9. Which of the following shapes is an exception to the normal practice of placing seams on the shortest side in sheet metal development?
A. Cone
B. Cylinder
C. Elbow
D. Pyramid
8-10. In what type of development do the slanting lines of pyramids and cones not always appear in the true lengths?
A. Orthographic-perspective
B. Parallel-line
C. Radial-line
D. Triangular
8-11. Concerning radial-line developments, which of the following statements is true?
A. A line parallel to another line is an equal distance from that line at all points
B. A line perpendicular to another line will intersect at only one point
C. The lines radiate from the apex of a cone
D. When finished, the lines form a three-dimensional drawing
8-12. In a radial-line development, the reference lines are transferred from what view to the development?
A. Front
B. Rear
C. Side
D. Top
8-13. In a radial-line development of an oblique pyramid, what measurement must be found first?
A. Apex height
B. Base
C. Frustum height
D. Lateral edges
8-14. What type of development is slow and difficult to draw?
A. Orthographic-perspective
B. Parallel-line
C. Radial-line
D. Triangular
8-15. When using triangular development, to find the true length of the varying oblique lines, what type of diagram is drawn?
A. Block
B. True length
C. Reference
D. Architect scale
8-16. Which of the following items is an example of using triangular development?
A. Rectangular box
B. Straight connections
C. Transition pieces
D. Truncated pyramid
8-17. In drawing an oblique cone, the elements are first drawn in which of the following views?
A. Front
B. Rear
C. Side
D. Top
8-18. Which of the following is the first step in developing a square-to-round transition piece?
A.
B.
C.
D. Establish reference lines Create a true-length diagram Develop the top view Draw a semicircle
Review Questions
8-1 For which of the following reasons should the sheet metal development drawings allow additional material?
A. Compression during shaping
B. Damage to the material
C. Joining of edges
D. Miscalculations
8-2. When drawing a lap seam, the allowance must be how many times the diameter of the rivet being used?
A. 1
B. 3
C. 5
D. 7
8-3. If the finished part is not shown with the development, what item should be included?
A. A scale model
B. Drawing instructions
C. Color code list
D. Marking instructions
8-4. Which of the following terms describes the amount of material consumed in making a bend?
A. Base measurement
B. Bend allowance
C. Bend tangent line
D. Setback
8-5. The three procedures commonly used in developing patterns are parallel-line, radial-line, and what other type of development?
A. Circular
B. Perspective
C. Rectangular
D. Triangular
8-6. Which of the following statements defines parallel-line development?
A. The development of an object that has surfaces on a flat plane of projection
B. The development of an object that has surfaces on a slanting plane of projection
C. The first series of prints used in construction and manufacturing
D. The perspective print of the development of parallel roadways
8-7. The parallel-line development is based upon which of the following principles?
A. A line parallel to another line is an equal distance from that line at all points
B. A line perpendicular to another line will intersect at only one point
C. The lines radiate from the apex of a cone
D. When finished, the lines form a three-dimensional drawing
8-8. What type of development is used when an object has the same cross-sectional shape throughout the length?
A. Orthographic-perspective
B. Parallel-line
C. Radial-line
D. Triangular
8-9. Which of the following shapes is an exception to the normal practice of placing seams on the shortest side in sheet metal development?
A. Cone
B. Cylinder
C. Elbow
D. Pyramid
8-10. In what type of development do the slanting lines of pyramids and cones not always appear in the true lengths?
A. Orthographic-perspective
B. Parallel-line
C. Radial-line
D. Triangular
8-11. Concerning radial-line developments, which of the following statements is true?
A. A line parallel to another line is an equal distance from that line at all points
B. A line perpendicular to another line will intersect at only one point
C. The lines radiate from the apex of a cone
D. When finished, the lines form a three-dimensional drawing
8-12. In a radial-line development, the reference lines are transferred from what view to the development?
A. Front
B. Rear
C. Side
D. Top
8-13. In a radial-line development of an oblique pyramid, what measurement must be found first?
A. Apex height
B. Base
C. Frustum height
D. Lateral edges
8-14. What type of development is slow and difficult to draw?
A. Orthographic-perspective
B. Parallel-line
C. Radial-line
D. Triangular
8-15. When using triangular development, to find the true length of the varying oblique lines, what type of diagram is drawn?
A. Block
B. True length
C. Reference
D. Architect scale
8-16. Which of the following items is an example of using triangular development?
A. Rectangular box
B. Straight connections
C. Transition pieces
D. Truncated pyramid
8-17. In drawing an oblique cone, the elements are first drawn in which of the following views?
A. Front
B. Rear
C. Side
D. Top
8-18. Which of the following is the first step in developing a square-to-round transition piece?
A.
B.
C.
D. Establish reference lines Create a true-length diagram Develop the top view Draw a semicircle